Bitcoin and the Quantum Problem – Part I: Discrete Logs are Hard

This is Part I in a 3-part series on Bitcoin and Quantum Computing. Find Part II here:

Bitcoin and the Quantum Problem – Part II: The Quantum Supremacy

---

Quantum computing is, in my opinion, the biggest risk to Bitcoin. It’s a big looming problem for a lot of financial systems, and for various other blockchains too, but it’s kind of a uniquely big and intractable problem for Bitcoin. I have been developing these views for some time and recent developments have only further convinced me that this needs to be treated some urgency and seriousness. In this series I lay out how Bitcoin works, why I think quantum is a real and particularly challenging issue for Bitcoin specifically, and various post- quantum break scenarios.

Before we get into quantum, though, we need a brief refresher on how and why Bitcoin is secure.

I’m going to explain Bitcoin’s cryptographic security first in three ways:

1. a literal protocol-y way

2. a visual, mathematical way; and

3. via analogy.

Building intuition around elliptic curves is very hard. I’m sure there are some mathematicians who great intuition around it. Truthfully I didn’t before writing this article. I just took it for granted that the cryptography worked.

(This section is giving me a real “If you wish to make an apple pie from scratch, you must first invent the universe” feeling. I am struck by how many load-bearing cryptographic techniques are involved in a “simple” bitcoin keypair, and I don’t have time to recursively explain all of them.)

Bitcoin from the protocol perspective

You start with randomness (entropy). Simply speaking, you think up a really big number between 1 and 2²⁵⁶.¹ Let’s use the SHA256 hash of “example”² to generate a toy private key. That gives you a 256-bit integer. This is your private key:

50d858e0985ecc7f60418aaf0cc5ab587f42c2570a884095a9e8ccacd0f6545c

You then take this integer and use it as an input into a special curve equation that we’ve all agreed to use for ECDSA called secp256k1. What you do specifically is (in an elliptic-curve, scalar way) multiply the private key k with G, a known point in the secp256k1 curve we’ve all agreed on. What you’re actually doing here is adding G to itself k times, on this specific elliptic curve.

The output of k * G is your public key. In our example, our public key in hex is

02 4033389cf6632a172546748fda79e7fbabce944b552db5dba81b16c01fec377b

For a legacy address in P2PKH format, you then hash the public key twice (once with SHA256 and once with RIPEMD) and in this case you get:

17oFBXabB2LLgDoUfu5P5bPxWvNepHQ96T

This is your pay-to-public-key-hash bitcoin address. If you’ve used Bitcoin it should look familiar. It’s not the only address format and not the only digital signature that we use in Bitcoin. Since 2021, we also have Schnorr signatures, which use the same elliptic curve (secp256k1) but are simpler and have some other useful properties.

Assume your address has some Bitcoin associated with it. More precisely, assume the Bitcoin UTXO set contains some unspent transaction outputs (UTXOs) that list YOUR address in the locking script. That’s what we talk about when we talk about “owning a Bitcoin” – knowing the private key corresponding to the public key whose hash the bitcoin blockchain lists as being able to satisfy the spending conditions to un-encumber some units of Bitcoin, if you provide a valid signature.

In more literal terms, a UTXO in the blockchain might look something like this:

value: 0.50000000 BTC

scriptPubKey: OP_DUP OP_HASH160 4a8fba212554eac0a6f956d7d34ef783a7a16ca2 OP_EQUALVERIFY OP_CHECKSIG

The hash “4a8f…” is a 20-byte hash of your earlier compressed public key.

To spend a P2PKH output, you must provide (to the other participating nodes) a signature and your public key. Your wallet, which still has knowledge of your original private key (“50d858e…”) produces an ECDSA signature over the hash of the transaction data (some administrative stuff, the previous UTXO script, and the outputs you’re creating – as in, where you’re sending how much BTC).

The other nodes on the Bitcoin network that receive your transaction duplicate the public key -> address transformation by hashing the public key which you broadcast and making sure it corresponds to the hash that exists on the blockchain. They then verify the signature you’ve posted against the pubkey and the transaction hash. In plain language, when you publish a signature, you are saying “I know the private key corresponding to the public key whose hash locks the UTXO I’m spending.”

Even though you can receive transactions to your address (“17oFB…”), you have to actually broadcast the public key (“02 4033389…”) when you want to spend the coins. This is important, remember this for later.

Ok, so that’s a very mechanical explanation of how Bitcoin works, but it leaves us with little intuition. What we’re really interested in is understanding why and how the discrete log problem is hard.

Bitcoin’s cryptographic security in a visual way

(I have no background in math beyond doing stats and econometrics in my graduate program. It’s entirely possible I’m making mistakes here. For alternative primers on ECC/ECDSA see here, here and here).

The actual elliptic curve used in ECDSA is called secp256k1 and it is defined as:

\(y^2 = x^3 + 7 \pmod p\)

Where p is the following prime number:

\(p = 2^{256} - 2^{32} - 977\)

The “curve” sits on a very large field, bounded on both axes by p. If you end up with a coordinate which is larger than p, you simply divide by p and keep the remainder, staying in the finite field.

The mod in mod (p) is short for modulo, which is fancy math talk for “the remainder after a certain number is reached,” or in more simple terms, “wrapping around”. We actually do modular arithmetic all the time, when we count time. On a clock, we count “mod 12”. If it’s 10 am and we want to add 5 hours, we hit 12 and wrap around to 3pm, not onwards to 15 (unless we’re in Europe).

In the clock example, we are doing (10 + 5) mod 12 = 3.

Modular arithmetic ensures that the “game” we are playing happens on a finite “map”. We need this so computers can make sense of everything. But unlike in a video game, it’s a map where if you hit the edge, you instantly teleport to the other side.

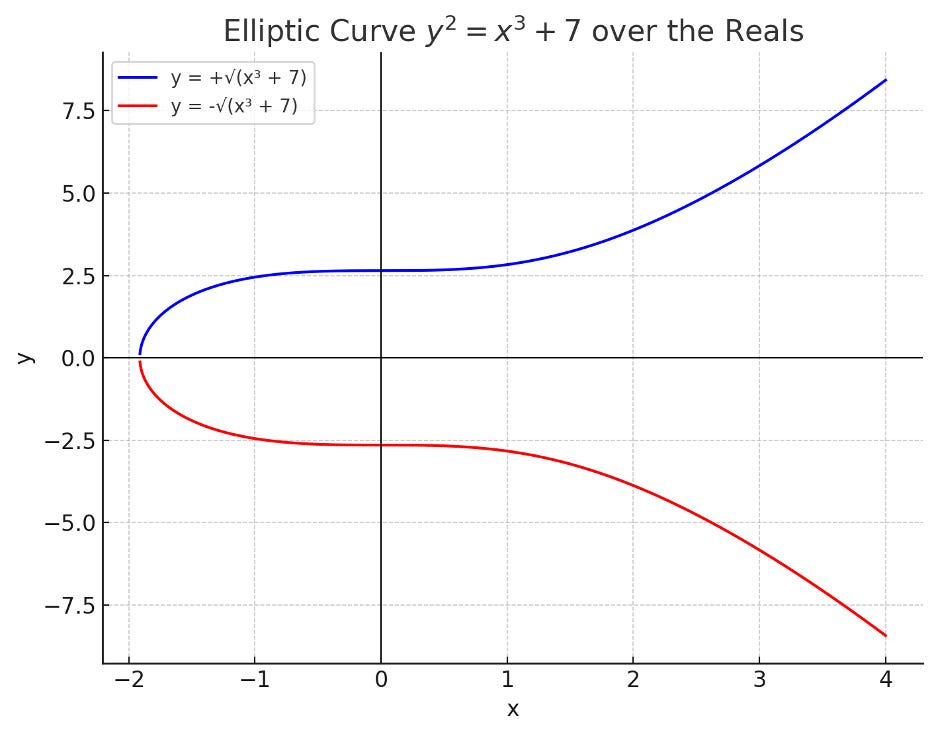
Plotting at the elliptic curve y² = x³ + 7 not modulo anything, but simply plotted over real numbers, gives us this:

Bitcoin’s curve doesn’t look anything like this though. By making the secp256k1 curve modular (or “discrete”) we are setting clear rules for the “game” so everyone is on the same page and computers can do the math without weird infinities and edge cases.

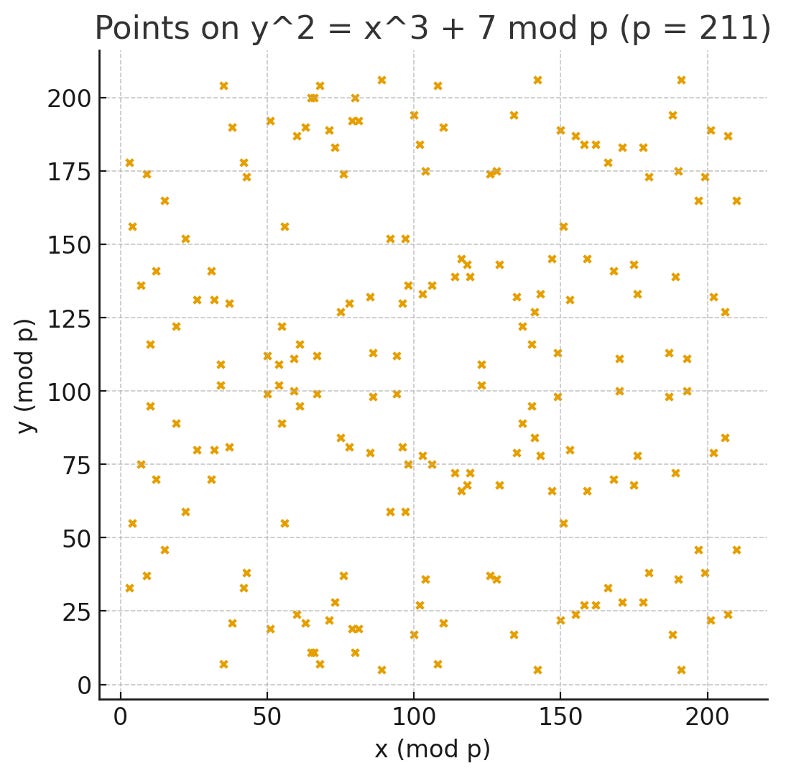
Once you define the curve group over a finite set of numbers with the prime modulus, you get a curve that looks more like this:

Keep in mind that this curve has a modulus of 211, whereas secp256k1’s modulus is ~2²⁵⁶.

For this reason, you can’t really “look” at Bitcoin’s curve. In fact, you literally can’t. Let’s say you tried to depict a portion of Bitcoin’s elliptic curve on a standard HD screen with ~2m pixels where one pixel equals one integer. Bitcoin’s grid stretches over 10⁷⁷ x 10⁷⁷ possible integers. So you’re only rendering a minute fraction of the curve space (10^-74). No points at all would show on your screen. You’d have to zoom out by 10³⁵ on each axis before you could expect to see a single point.

Bitcoin land is big. And invisible.

For the sake of intuition, let’s return to the more intelligible elliptic curve defined over the set of real numbers, with no modulus.

Recall from earlier that we are picking a private key k (a random large number) and then multiplying set starting point G by itself k times. So we are multiplying k * G but really in elliptic curve land we are adding G to itself k number of times.

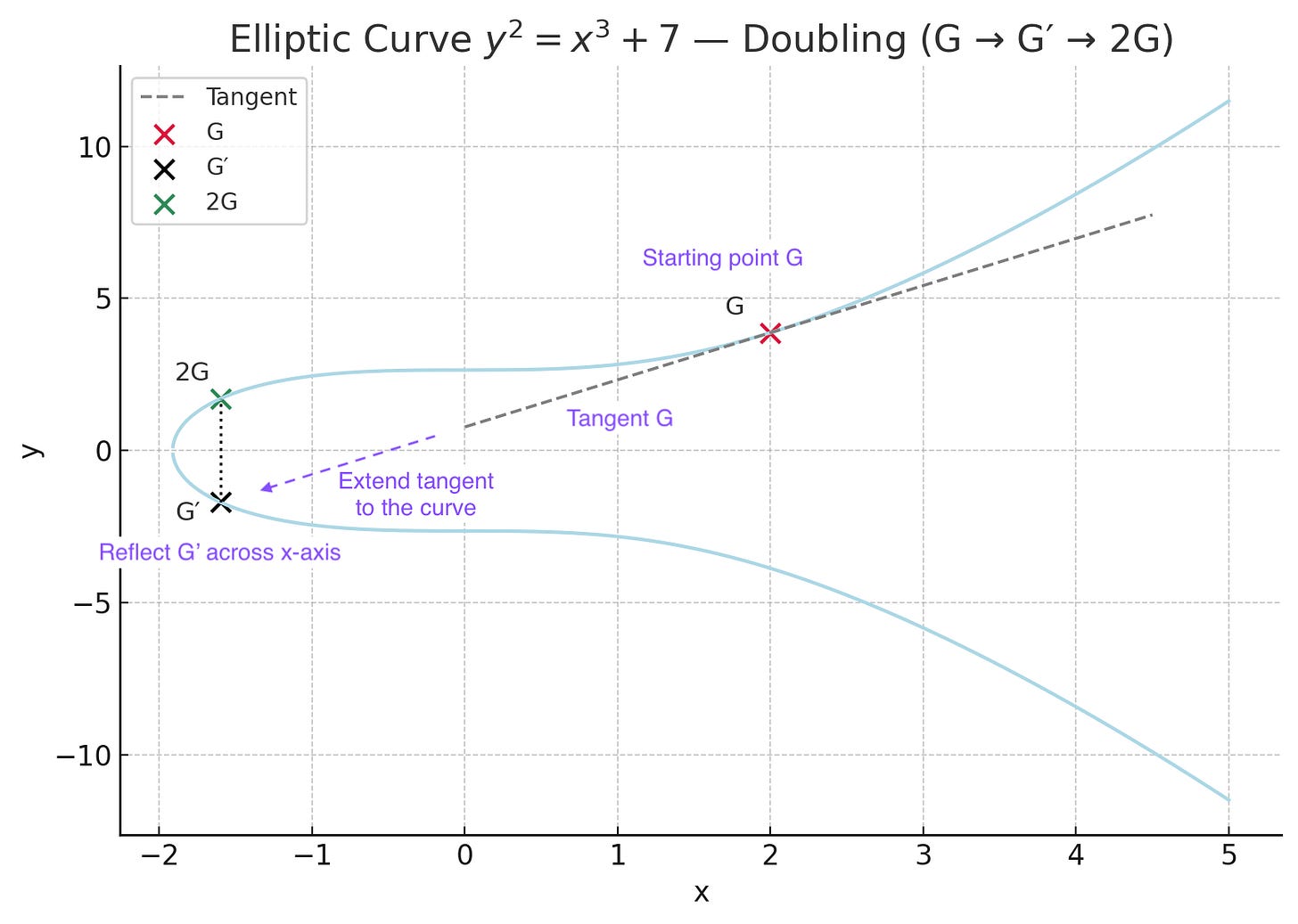
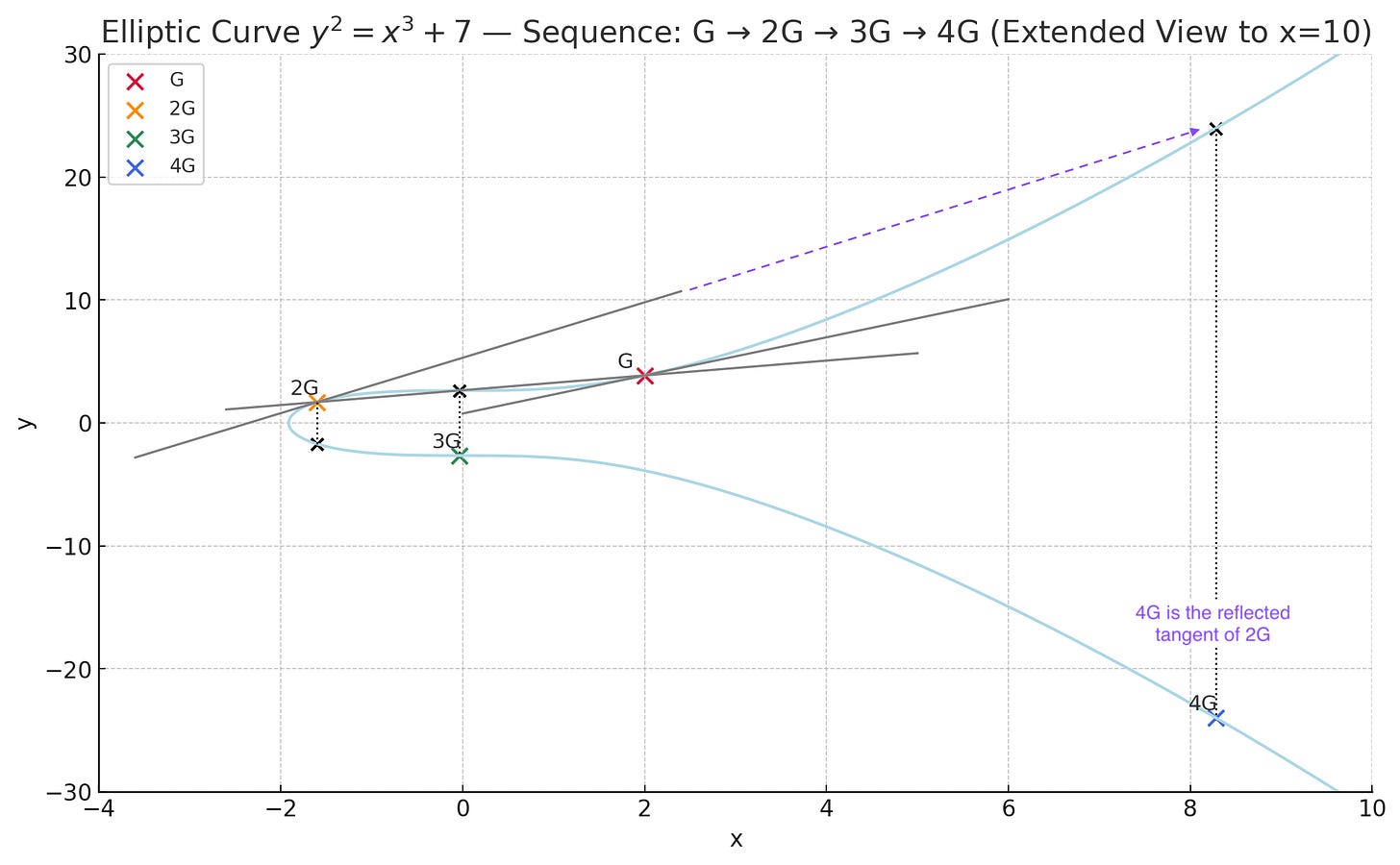
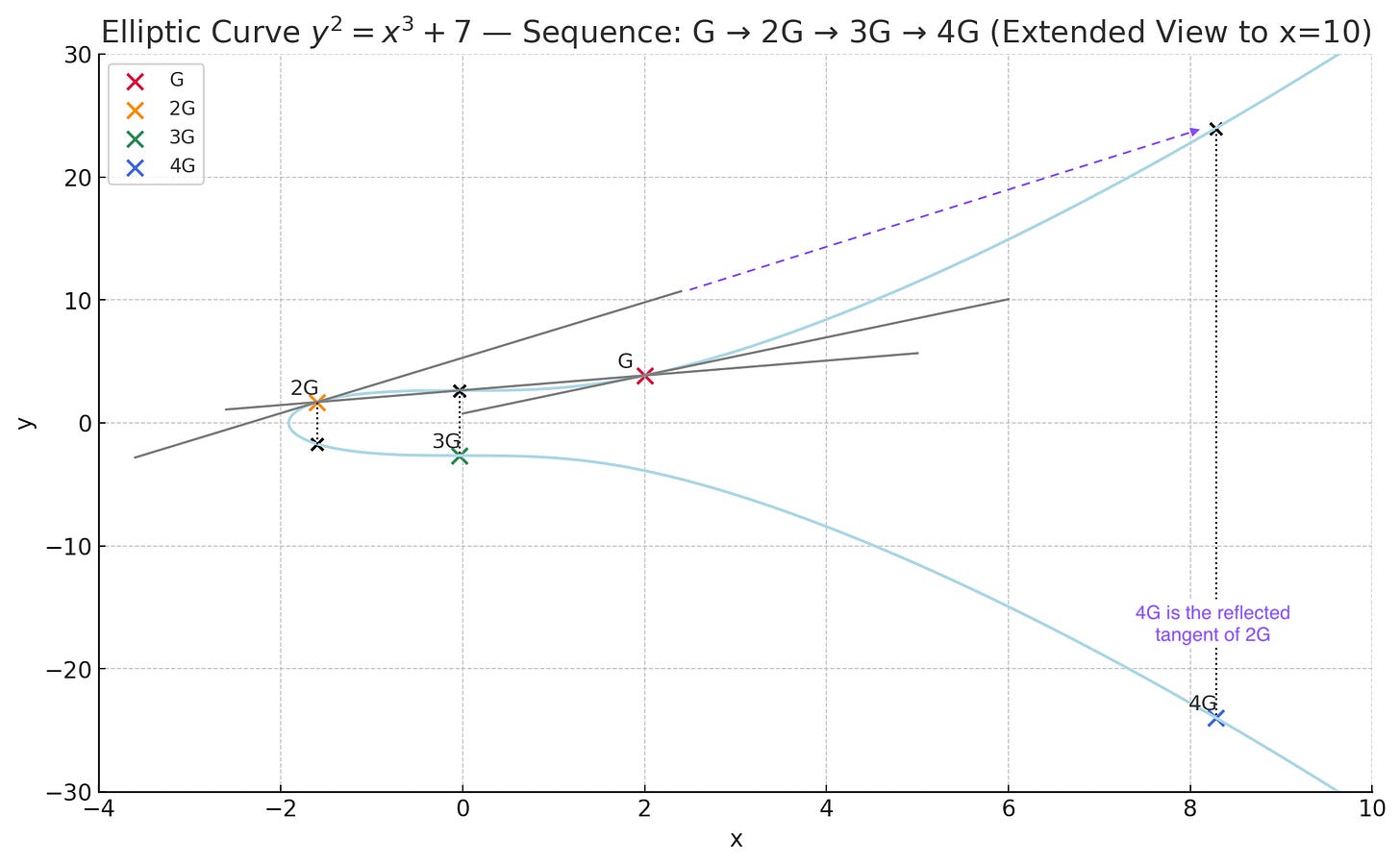
Visually, this is what it looks like. The “game” is to add various points together and make progress by moving around the curve (unpredictably). The way you “add” points in a geometric sense on elliptic curves is to draw a line between them, find the point where that line intersects the curve, and invert that point over the x axis. (This works because there is a rule in algebraic geometry that says that any non-vertical line intersects an elliptic curve exactly three times.³) When you are adding the same point to itself, you take the tangent of the curve. You can build intuition for why we take the tangent if you think about drawing a line between two points on a curve that are very close together.

Recall that we want to multiply G by k, or add G to itself k times.

First, we add G to G by taking its tangent. We follow this line until it hits the curve again, and then reflect it over the x axis. (The entire curve is symmetrical.) This new point is 2G.

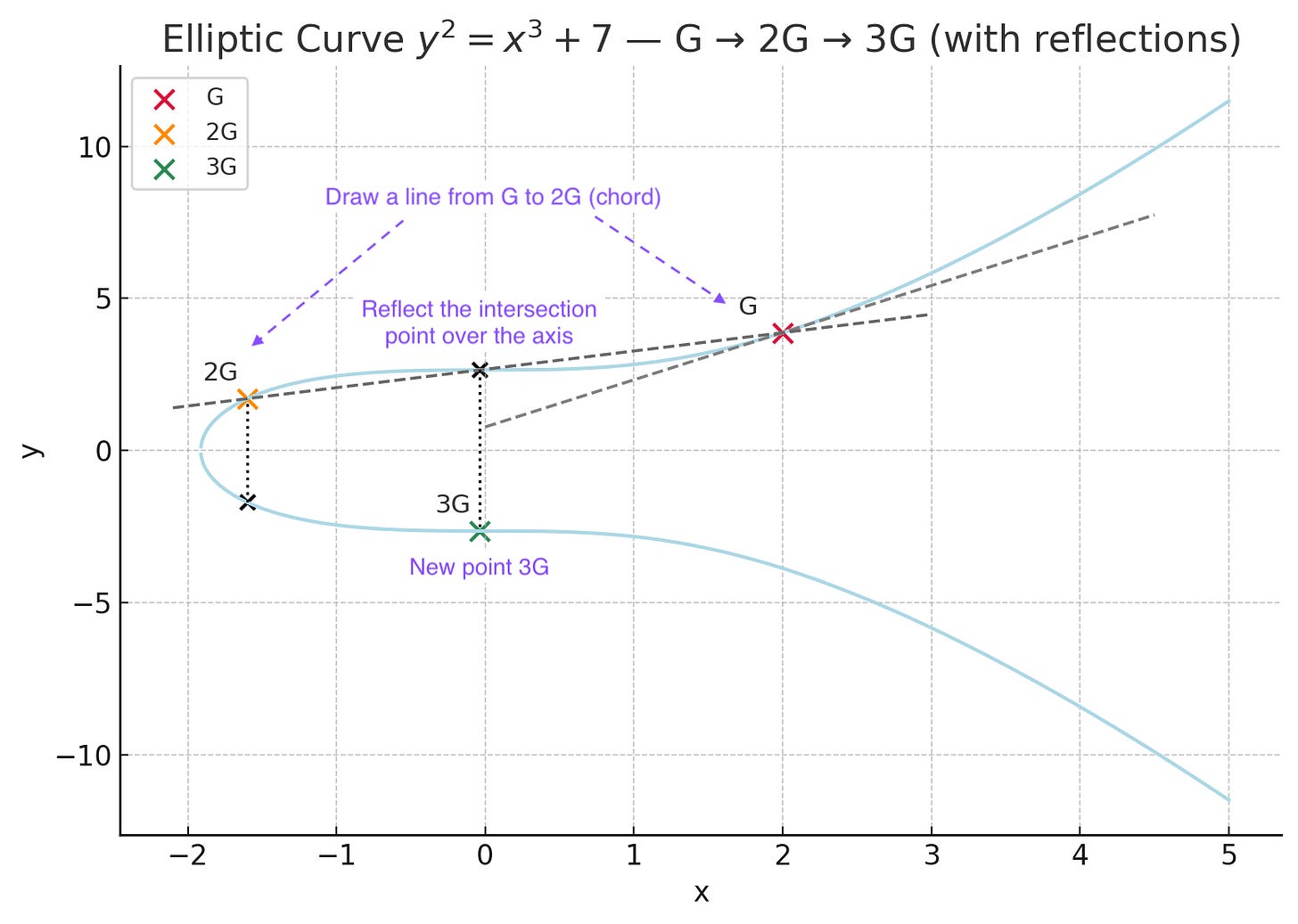
Once we have 2G, we want to keep adding G’s. So we simply add G to 2G, and we do this by drawing a line (or the “chord”) between G and 2G, finding the intersection point, and again reflecting this over the x axis. That gives us 3G.

The thing to remember is that when you’re incrementing to an odd number, you have to add +1G using the point-to-point (chord) method. However, when you are going up to an even number (2G to 4G), you can skip ahead and double your point to itself. We represent this geometrically with a tangent, even though in Bitcoin-land this doesn’t make visual sense as we are just dealing with a field of points. Rest assured though, the tangent math still works algebraically.

If we continue our progression to get to 4G you can see that instead of going from 3G to 4G, we can instead simply double 2G to get to 4G by taking the tangent of 2G. (You’ll notice that you can also get to 4G by adding G to 3G with the chord rule.) Pay attention to this, it’s important.

So in our simplified model, after adding G to itself k number of times, you get to a set of coordinates on the grid, which is our public key. For instance if your private key was simply 4, with the starting position G being (2, 3.87) on this chart your public key would be 4G or (8.27, -23.96). In ECC, a third party would have to try and guess the number of steps you took to get to those coordinates – with no way to reverse-engineer it aside from simply brute forcing it (starting at known coordinates G and counting hops until they happened to stumble on the public key). But as discussed, this is computationally infeasible.

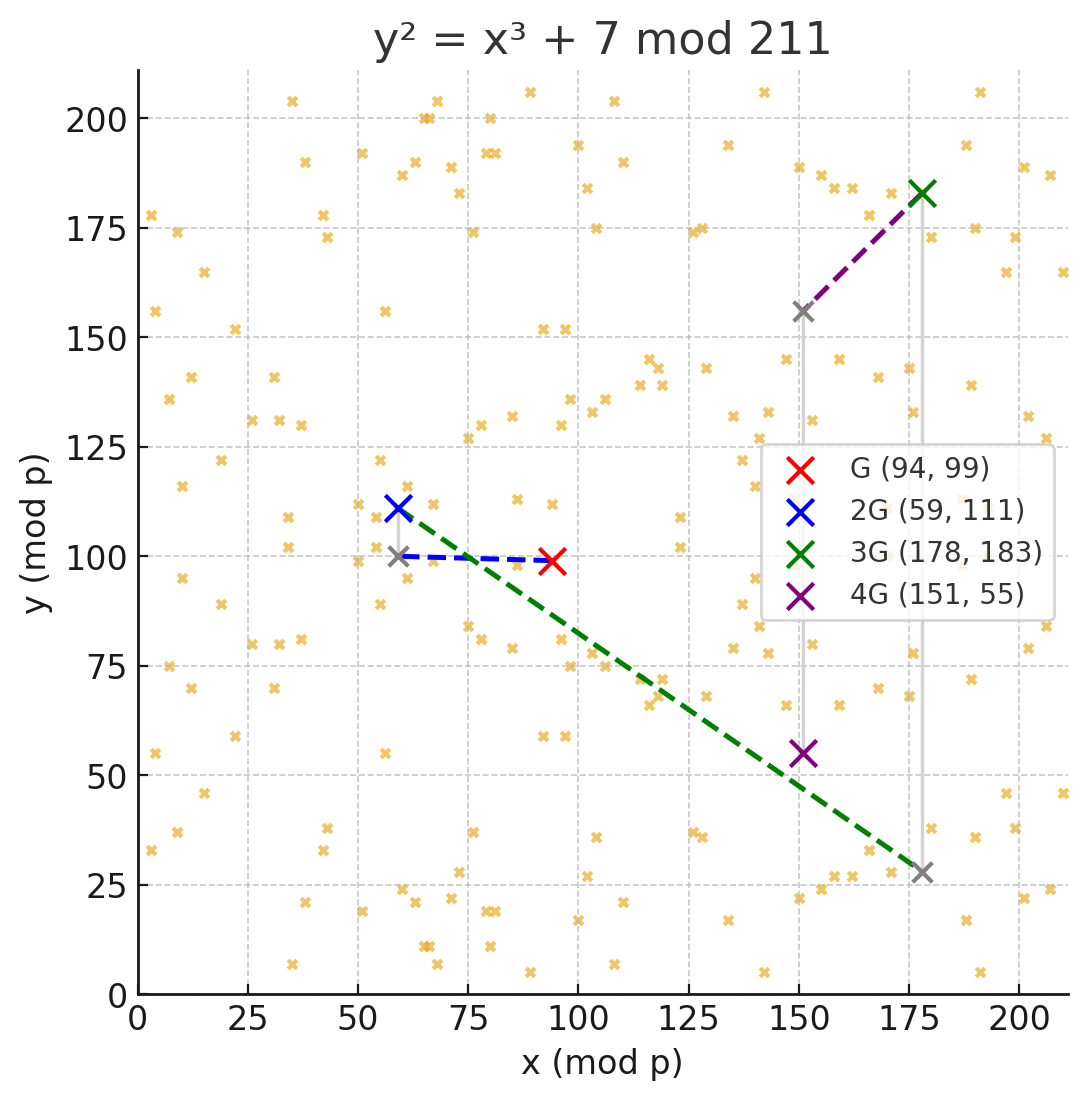
To give you a more concrete sense of the “scrambling” happening in true elliptic curve groups, lets look at our simplified modulated example from earlier. This is a minuscule example that sets the modulus at 211 instead of ~2²⁵⁶. Here we start at G (94,99) and perform the same exact scalar multiplication process we described above, just that it’s happening on the discrete, discontinuous field of integers.

As before, we take the tangent of G until we hit the curve again at (59, 100). We then reflect over the x axis to find 2G (59, 111). We repeat the process by adding G to 2G to find 3G and so on. It should be easy to understand at this point why it might be hard to find k given an arbitrary multiple of G.

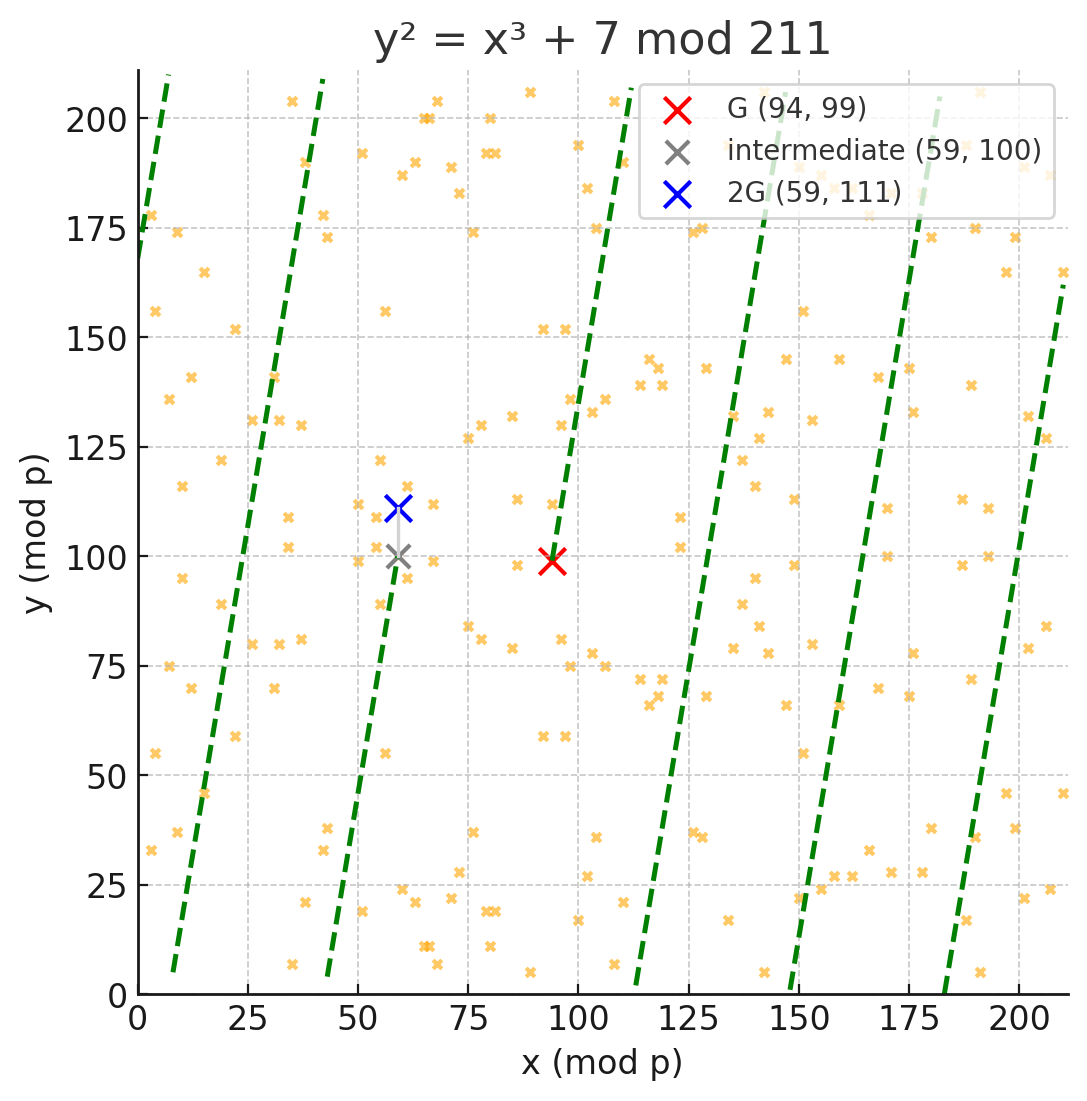
It’s harder of course to tell why the tangent of G would lead us to 2G, since there’s no visible curve here, just a cloud of points. But the same thing is happening. Here I’ve depicted exactly what’s going on when we simply go from G to 2G:

You can see clearly how to the modular arithmetic scrambles the output as we advance from G to 2G. We wrap around the defined plot area multiple times in search of the next valid point. In Bitcoin-land, most scalar operations that we undertake as part of ECC wrap around too – even though the Bitcoin plot is inconceivably large.

(One quick note on the intuition here. The line isn’t “jumping” from the top to the bottom. What we’re actually looking at is a 2D representation of a torus, which is a geometry word for a donut. It only looks like it’s jumping because we are staring at a flattened out version of a 3D object. Imagine gluing the top and bottom edges to each other, so you have a cylinder, then gluing the right and left to each other, to make a donut shape. If you traced a helix around the outside of the donut with a pen, and then unrolled it back into flat paper format, it would look something like this.)

Ok, back to the simplified, real number example.

You might be wondering to yourself – well if incrementing k times in the elliptic curve costs an unholy number of operations, how is the public key derived efficiently in the first place?

And this is where the visual really shines for me.

As you see in the chart again, there’s two ways to get to 4G. You can add 3G to G, plot the line between the two points, and reflect it across the x axis when you hit the curve. Or, you can simply double 2G, taking the tangent and doing the same reflection when you hit the curve. The tangent “doubling” operation is an insane short cut!

Think about if you wanted to get to 13G. You could add G to G, add 2G to G, and so on. Or you could go G + G (2G), 2G+2G (4G), 4G+4G (8G), 8G+4G (12G), 12G+G (13G). That’s only 5 operations (3 doublings and 2 additions) instead of 12 point additions. (See here for a visual depiction.)

This might seem trivial but it starts to really matter when you are staring 2²⁵⁶ operations in the face.

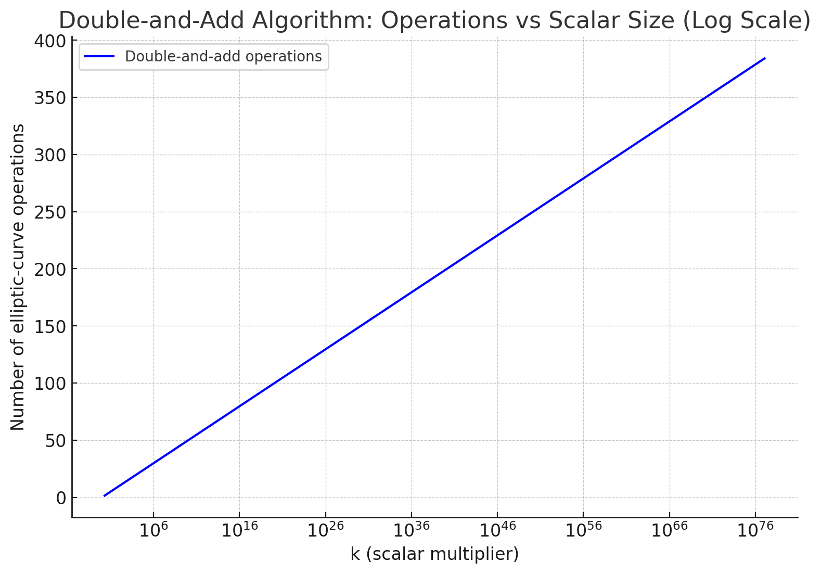
In our above toy model, we can call our tangent operations “doubling” and our point-to-point operations “adding”. As it turns out, there’s an algorithm called “double-and-add” that takes advantage of the doubling shortcut. It accomplishes in 384 elliptic curve operations what would otherwise require an infeasibly many ~2²⁵⁶. Quite the efficiency gain. (A conceptually similar algorithm was first found on an Egyptian scroll called the Rhind Papyrus which dates to 1650 BC.)

The way it works is exactly as described above. Instead of tediously adding G to G 10⁷⁷ times, you process the bits of k one at a time, sometimes doubling (tangent rule), sometimes adding (chord rule). To process 256 bits, we need to do 256 doubles and around 128 adds. We don’t actually iterate through all the multiples of G. We skip ahead.

In complexity notation, you would write the “naïve” method of simply adding G to G k number of times as O(k) – the work required scales with the size of k. By implementing double-and-add, we massively reduce the work to O(log(k)) – depicted above.

But why is there no point division, if we’re doing point multiplication, you might ask? After all, all we’re doing is k * G = P where k is your private key, G is the known starting point, and P is the public key. Since G and P are known, why not simply divide P by G to get k, you might ask?

The answer is that elliptic curve “multiplication” isn’t actually multiplication at all. As we’ve demonstrated, it’s actually repeated addition. We have just found clever ways to speed up the addition so we can skip a lot of steps.

Inverting this process – finding k given P and G – is the discrete logarithm problem itself. Bitcoin’s cryptographic security is based on that problem being hard.

More generally, the reason it’s hard to reverse point addition in the elliptic curve is because of its structure, and this is why elliptic curves were specifically chosen for this. The equation mixes a cubic and a quadratic variable, which makes it nonlinear and hard to invert algebraically. Moving over from real numbers to finite fields means you can no longer use calculus to get a sense of direction, distance, or slope. There’s no “which way is closer” or “how fast am I approaching the target” – every step is a blind jump in a featureless, discontinuous space.

Because you are wrapping around the modulus with almost every operation, there’s no “progress” visible on the graph. Where you are at any given point gives you no information about how many “spins” you have undertaken. Unwinding it is like turning a cake back into its ingredients or a smoothie back into fruit. The elliptic curve multiplication process is a gigantic, one-way, deterministic number scrambler.

Bitcoin’s cryptographic security in natural language

When I first started writing this post I thought I would do the mechanical and then the more mathematical explanations as a preamble to the natural language section which would really drive intuition. But having been through the laborious process of working out the geometric explanation above I actually feel pretty good about the math. Nevertheless, if you’re not there yet, let’s consider two analogies that might help you if you are still feeling lost.

Imagine a circular one-mile racetrack. You are driving a specially configured car that generates exactly the same amount of thrust with each press of the gas pedal. The unusual thing about this racetrack is that you can only occupy a finite set of positions on it. There are thousands of tiny markers arranged on the track, allowing you to know with extreme precision exactly where you are. When no one is watching, you hit the gas a certain number of times, and loop around the track a bunch of times, leaving your car parked on the track. Your public key is the location of the car, G is the fixed thrust generated by the gas pedal, and your private key is how many times you pressed the gas. You’ve looped around the track so many times, and there are so many possible positions on the track that it’s virtually impossible to tell how many times you pressed on the gas just by looking at where the car is parked. The only way to figure it out as a third party is to get in the same car, head to the starting line, and press the gas and loop around the track until they end up at the exact same position as the original driver. But this might require years – or centuries – of looping around and around.

But there’s no asymmetry in this analogy. The private to public key transformation is still brute force, so we need a speedup, just like the log-time scalar multiplication in Bitcoin.

Now imagine that the car has a lazy driving mode. It’s still configured the same way as before – each press of the gas pedal generates a fixed amount of thrust and moves you around the track a predetermined distance. But there’s now an optional autopilot feature in the car that doubles the prior distance every time you engage it. So you can combine the longer autopilot stretches with the ordinary pedal presses to get to the same k, just with many fewer pedal taps. Based on your target k, you can actually pre-plan your trip in advance. Now to get to k = 13, you only have to press the pedal 6 times – three ordinary taps, and three autopilot doublings. The magic of scalar multiplication in elliptic curve world is that these long taps take just the same amount of time as the short taps, even if a long tap is driving you 10⁵⁰ times further. And the guy trying to reverse-engineer your final position can’t use lazy driving mode. He doesn’t know the sequence of long and short taps that got you there, so he has to drive the whole track manually – checking his position against yours after every single tap.

If that didn’t do it for you, let’s try another. Suppose you have a freshly ordered deck of cards. That’s starting point G. You shuffle it in exactly the same way k number of times. K is your private key. That gives you a nicely shuffled and random-looking deck. The order of cards in the shuffled deck is your public key. No matter what, if you shuffle the same fresh deck k number of times, you’ll end up exactly at the same deck configuration.

From inspecting the shuffled cards, there’s no way someone else could guess how many times you shuffled them. The only way to “reverse engineer” the shuffle count is simply to replay it yourself, starting from the fresh ordering, and tediously shuffling over and over until you get the same result. To take it a step further, the original shuffler (the person deriving the keypair) has access to a card-shuffling machine that can shuffle many times faster than a human. But the person trying to figure out your private key can only shuffle at human speed. And no one can shuffle “backwards”.

Interestingly, a deck of cards actually has less entropy than secp256k1 – 2²²⁶ versus 2²⁵⁶ bits.

Unfortunately, I can’t help build intuition around how digital signatures (and third-party verification of those signatures) work, because they are much more complex and unlike anything that exists in the real world. This is a shame, because signatures are an essential part of how Bitcoin works, beyond just initial key derivation. In plain language, a signature is the specific computation that only someone who knows the private key could produce, and that everyone else can verify with just knowledge of the public key.

There aren’t many good analogies for this, and it’s far more complicated to explain than elliptic-curve multiplication, which is the more fundamental concept anyway. We can mostly skip a long discussion of signatures since they depend on the one-way-ness of the ECC function is the most important thing, and that is the thing that is threatened by a practical quantum computer. ECDSA and Schnorr are both based on the elliptic curve discrete log problem being hard generally, and secp256k1 specifically.

Bitcoin’s entire cryptographic premise is “there exists a one-way function that’s easy to compute in one direction, and infeasible to invert.” We’ve never had to worry about this before, because it’s such an ironclad assumption in cryptography.

Until now.

---

1. This isn’t precisely correct. The actual valid private key range for ECDSA in integer terms is the space between 1 and 115792089237316195423570985008687907852837564279074904382605163141518161494337, which is close to but not exactly 2²⁵⁶. This is like picking a random atom in the universe (actually, a universe much bigger than ours) – you can be pretty sure that no one else is going to accidentally pick the same one as you.

2. Obviously, don’t do this. “Example” is not enough entropy for a secure Bitcoin keypair.

3. This is annoyingly only sort of true. We need infinity to make it true.